0.1+0.2=?

0.1+0.2=?

相信写过程序的人都知道，0.1+0.2≠0.3，而是等于0.30000000000000004，类似的还有 0.7×180=125.99999999998，1000000000000000128 ===1000000000000000129。

虽然很久之前就知道这个结果，也知道该怎么去做，但是一直没有去深究其中的原因，今天来复习一下其中的相关知识，顺便做个笔记。

众所周知 JS 仅有 Number 这个数值类型，而 Number 采用的是 IEEE 754 64位双精度浮点数编码。这是一个什么样的标准呢？使用这个标准的 64-bits 双精度意味着什么？所以，要掌握 JavaScript 中的数字，我们首先得了解 IEEE 754标准。下面，我将尝试说明一下这个标准，为我们最后学习 JavaScript 中的数字做铺垫。

当下，计算机如此普及，我相信，即便非程序员也了解：计算机的世界只有 0 和 1。而一个程序员应该了解：0 / 1 组成的东西叫机器码，有原码, 反码, 补码等。而一个 JS 程序员应该了解：JS 中的数字是不分类型的，也就是没有 byte / int / float / double等的差异。而一个稍微研究 ES 规范的 JS 程序员应该了解：JS 的 number 是 IEEE 754标准下 64-bits 的双精度数值，而且 ES 中有 ToInteger / ToInt32 / ToUint32 / ToUint16 等 Type Conversion。下面，我们就尝试着讨论一下这些。

从硬件的角度上讲，维护两个状态是相对容易的，比如一个二极管的导通或者截止，一个电脉冲的高或者低，从而在实现集成电路时候可以更加简单高效，所以计算机普遍使用 0 和 1 来存储和计算。那么，只有 0 和 1，如何表示 1234567890 呢？这就涉及到 机器码 和 真值。

机器码和真值

所谓 机器码 是指，整数在计算机中二进制形式。规则很简单，机器码的最高位（左第一位）表示数字的正负，0 表示正数，1 表示负数，其余位按照进制转换的规则表示具体数字。

所谓 真值 是指，机器码按照上述转换规则还原的带有正负的实际整数。

举例而言，用 8-bits 表示一个整数，则十进制的整数 +6 可表示为：00000110；十进制的数字 -5 可表示为 10000101。这里说的 +6 和 -5 便是 真值，而表示它们的二进制数便是 机器码。再次注意，最高位只用于表示正负，比如 10000101 的真值是 -5 而非 133，以及我们关于机器码和真值的讨论是基于整数范围的，浮点数在计算机中的存储方式与整数有很大差值，将另作讨论。

有了机器码，我们便可以在计算机中使用机器码存储和计算真值，那么机器码在计算机中是如何计算的呢？

原码、反码、补码

机器码分为多种，主要包括原码、反码、补码、移码等，今天我们主要总结一下前三个，而移码非常简单，且多用于比较，不做详细说明。另外需要补充一点，我们在此区分机器码的这么多种形式，主要是针对的有符号数，而无符号数，不需要使用最高位来表示正负，也就不需要这么多种编码方式。

原码：

最高位表示正负，其它位表示真值的绝对值。其中，最高位为0表示正数或者0，为1表示负数。

比如，同样以 8bits 长度的数串表示 +7 的原码为 00000111，-7 的原码为 10000111。以后，我们会这样表示：

1
2
[+7] = [00000111]原
[-7] = [10000111]原

很明显，8-bits 的原码能记录的范围为：[-127, +127]。

原码的好处在于，易于理解，相对直观，方便人脑识别和计算。

对于原码，人脑使用，可以直接计算出其真值然后可以进行后续操作。但对于计算机，首先，因为最高位用于表示正负，所以不能直接参与运算，需要识别然后做特殊处理；其次，具体计算使用绝对值进行操作，所以两个操作数正负的异同会影响操作符，比如两个异号相加实际要做减法操作，甚至异号相减还需要判断绝对值大小然后决定结果正负。如此，我们计算机的运算器设计将会变得异常复杂。下面，我们将了解如何使用反码和补码将符号位参与运算，从而使加减法统一简单高效地处理，这也是反码和补码出现的原因。

反码：

正数的反码等于其原码，而负数的反码则是对其原码进行符号位不变，其它位逐一取反的结果。

比如，同样以 8-bits 长度的数串表示 +7，那么有如下：

1
2
[+7] = [00000111]原 = [00000111]反
[-7] = [10000111]原 = [11111000]反

同样，8-bits的反码能记录的范围为：[-127, +127]。

在按位取反之后，我们可以有下面的操作：

1
2
3
4
5
2 - 3 = 2 + (-3)
      = [00000010]原 + [10000011]原
      = [00000010]反 + [11111100]反
      = [11111110]反 = [10000001]原
      = -1

上面，我们将减法通过反码转化为了加法，如此，我们的运算将会简单很多，但是反码的方式同样存在一些问题：

1
2
3
4
5
6
3 - 3 = 3 + (-3)
      = [00000011]原 + [10000011]原
      = [00000011]反 + [11111100]反
      = [11111111]反
      = [10000000]原
      = -0

出现了 -0，这个值是没有意义的。另外，按照反码加法法则，如果最高位有进位，需要在最低位上+1，那么会出现：

1
2
3
4
5
3 - 2 = 3 + (-2)
      = [00000011]原 + [10000010]原
      = [00000011]反 + [11111101]反 (这里最高位有进位，需要在最低位+1)
      = [00000001]反
      = [00000001]原 = 1

这种情况，又增加了反码运算的复杂性，影响效率，为解决上面的问题，出现了补码。

补码：

正数的反码等于其原码，而负数的补码则是对其反码进行末位加 1 的结果。

比如，再同样以 8-bits 长度的数串表示 +7，那么有如下：

1
2
[+7] = [00000111]原 = [00000111]反 = [00000111]补
[-7] = [10000111]原 = [11111000]反 = [11111001]补

使用补码，继续做之前的操作：

1
2
3
4
5
6
7
8
2 - 3 = 2 + (-3)
      = [00000010]原 + [10000011]原
      = [00000010]反 + [11111100]反
      = [00000010]补 + [11111101]补
      = [11111111]补
      = [11111110]反
      = [10000001]原
      = -1

那么，如果是 3-3 呢？

1
2
3
4
5
6
7
3 - 3 = 3 + (-3)
      = [00000011]原 + [10000011]原
      = [00000011]反 + [11111100]反
      = [00000011]补 + [11111101]补
      = [00000000]补
      = [00000000]原
      = 0

是否还需要做额外的加法操作？

1
2
3
4
5
6
7
3 - 2 = 3 + (-2)
      = [00000011]原 + [10000010]原
      = [00000011]反 + [11111101]反
      = [00000011]补 + [11111110]补
      = [00000001]补
      = [00000001]原
      = 1

这样，我们便可以完美的将减法统一到加法之上，而且不需要繁琐的正负判断，进位控制，甚至可以节约一个位置。那么，这个位置，也就是 10000000 如何处理呢？按照规定，10000000 用来表示 -128，正数的补码 / 反码 / 原码相同，而负数的补码只是占用了 -0 的 [10000000] 原和 [11111111] 反转换后得到的 [10000000] 补表示 -128，但是这个只是帮助理解，不能反向回推得到 -128的原码和补码。

所以，8bits的补码能记录的范围为：[-128, +127]。

至此，我们已经了解了，计算机中主要使用的存储和计算整数的方式，鉴于现代计算机主要使用补码方式，自然能很容易理解各种数字类型的表示范围。这对于我们后面理解一些 JavaScript 中的极端情况至关重要。

IEEE 754标准

标准的基本原理：

我们知道，对于计算机而言，数字没有小数和整数的差别，也就是计算机中没有小数点的存在。虽然我们已经找到了很完美的整数存储计算的方案，但是当涉及到小数，我们很容易发现，现有的方案无法解决我们的需求。然后，计算机科学家们便尝试了多种方案，主要便是 定点数 和 浮点数 两种。

所谓定点数，是指小数点位置固定在数串中间的某个特定位置，点两侧分别为数字的整数和小数部分。比如用 8-bits 字长的数串，小数点固定在正中间位置，那么11001001和00110101分别表示 1100.1001 和 11.0101 两个数字。这种方案简单直观易理解，但是存在严重的空间浪费，以及容易溢出的问题。

所谓浮点数，是指小数点的位置是不固定的，通过科学计数法（这个应该不需要解释吧）的方式控制小数点的位置，表示不同的数字。这个表示方案便是IEEE 754标准使用的方案。IEEE 754标准是目前使用最广泛的浮点数运算标准。下面我们将主要讨论一下此方案。

现在，让我们想一下小时候学习的科学计数法，比如 -123.456 这个数字，转换成科学计数法应该是：-1.23456 × 10^2。这里面已经包含了IEEE 754标准的主要元素。我们梳理一下：第一个，自然是正负号的问题，需要一个标志；然后，需要一个具体的数字，表示有效数字或者精度，如上例的 1.23456；再然后，需要一个控制小数点位置的数字，如上例的 10^2，回忆一下，我们学习科学计数法的时候，要求前面的数字的绝对值大于 1 而小于 10，也就是小于 10^2 中的底数(Base)，进制固定之后，底数应该是固定的，所以这里起决定作用的是指数，也就是上例中的 2。那么，有了这三个元素，我们便可以很轻松的表示出一个数字，并且灵活的调节小数点位置从而控制数字正负、精度和大小。

上面的要素，转换成标准语言描述，我们称表示正负的标志叫 符号（Sign），表示精度的数字为 尾数（Mantissa）或者 有效数字（Significand），而控制小数点位置的指数就叫 指数（Exponent），指数和 基数（Base）共同作用参与计算。下图取自wikipedia，我们直观地感受下这三个要素在一个数串中的相对关系（fraction区域即等同于前面说的有效数字区域）：

了解最基本的原理后，我们来大致看一下IEEE 754标准做了什么。

首先做的事情就是规定这三个要素在一个数串中占有的位数，试想一下，如果各个实现的位数不确定，那么我们是不是很难正确的还原出原始数字？IEEE 754标准规定了四种表示浮点数值的方式：单精确度（32位）、双精确度（64位）、延伸单精确度（43比特以上，很少使用）与延伸双精确度（79比特以上，通常以80比特实做）。只有32位模式有强制要求，其他都是选择性的。而现在主流的语言，多提供了单精度和双精度的实现，我们在此主要比较一下这两者，如图是它们各个部分对应上图，所使用的位数如下：

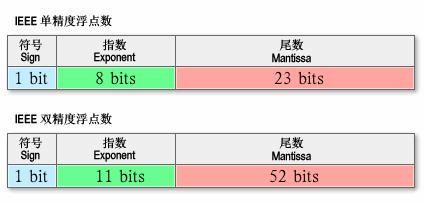
补充一点的是，无论是科学计数法还是标准的规定，都要求有效数字（不考虑符号位）必须 >=1 && <Base。所以，有效数字其实是一个定点数，小数点的位置固定在有效数字域的最高位和次高位之间。那么，按照上述规定，在二进制中，最高位只能是 1，所以标准要求省略其最高位，于是精度提高一位。比如，32-bits 的单精度有效数字区域只有 23 位，但是精度却是24位；64-bits 的双精度，拥有 52 位的有效数字域却是 54 位精度的。

然后，还有一个问题，如果按照先有的约定，是不是无法表示小于 1 的实数？因为，指数一定 >=0，有效数字一定 >1。于是，IEEE 754标准 提出了一个很重要的 指数偏移值。它是说明指数域(Exponent占用的区域)的编码值为指数的实际值加上某个固定的值，换言之便是，如果我们根据指数域计算出的指数是N，那么参与计算实际浮点数的指数应该是N-指数偏移值。根据IEEE 754标准的规定，该固定值为 2^(e-1) - 1，其中的 e 为存储指数的比特的长度。比如，从上图中我们看到，32-bits 的单精度是以 8-bits 表示一个指数域，那么偏移值应该是 2^(8-1) - 1 = 128−1 = 127。所以，容易得出，单精度浮点数的指数部分实际取值是[-127, 128]。比如，某个 32-bits 单精度的指数为十进制的 1，那么指数域的编码应该是10000001，某个 32-bits 单精度的指数域编码是00000001，那么该指数的实际值应该是十进制的 -126。这样，我们就能通过偏移值将正指数转换为负指数，从而使浮点数能逼近 0。浮点数的指数计算跟前面讨论的机器码恰好相反，正数的最高位都是 1，而负数的最高位都是 0。 以上的描述，便是IEEE 754标准最需要我们了解的原理部分，但是，作为一个广泛使用的工业标准，规定这些还是远远不够的。

稍加补充：

wikipedia对IEEE 754标准有如下描述：

这个标准定义了表示浮点数的格式（包括负零-0）与反常值（denormal number）），一些特殊数值（无穷（Inf）与非数值（NaN）），以及这些数值的“浮点数运算符”；它也指明了四种数值舍入规则和五种例外状况（包括例外发生的时机与处理方式）。

规约形式的浮点数：如果浮点数中指数部分的编码值在 0 < exponent < 2^(e-1) 之间，且尾数部分最高有效位（即整数字）是 1，那么这个浮点数将被称为规约形式的浮点数。也就是，严格按照我们上文描述编码的数字。

非规约形式的浮点数：如果浮点数的指数部分的编码值是 0，尾数为非零，那么这个浮点数将被称为非规约形式的浮点数。IEEE 754标准规定：非规约形式的浮点数的指数偏移值比规约形式的浮点数的指数偏移值大1.例如，最小的规约形式的单精度浮点数的指数部分编码值为1，指数的实际值为 -126；而非规约的单精度浮点数的指数域编码值为0，对应的指数实际值也是 -126 而不是 -127。实际上非规约形式的浮点数仍然是有效可以使用的，只是它们的绝对值已经小于所有的规约浮点数的绝对值；即所有的非规约浮点数比规约浮点数更接近 0。规约浮点数的尾数大于等于 1 且小于 2，而非规约浮点数的尾数小于 1 且大于 0。

上面的两个概念，几乎是直接从wikipedia上扒下来的，非规约形式的浮点数出现的意义是避免突然式下溢出（abrupt underflow），而采用渐进式下溢出。这已经是上世纪70年代的事情了，差不多是我的年龄的两倍了。这个是一些非常极端的情况，在此我尝试最简单地描述一下非规约形式的浮点数出现的意义，知道有这么回事便可：下面，以单精度为例，如果没有非规约形式的浮点数，那么绝对值最小的两个相邻的浮点数之间的差值将是绝对值最小的浮点数的 2^23 分之一，大家想一下，绝对值次小的浮点数减去绝对值最小的浮点数的值是多少？

1
2
3
1.00...01 × 2^(-126) - 1.00...00 × 2^(-126) = 0.00..01 × 2^(-126)
                                            = 1 × 2^(-126-23)
                                            = 2^(-149)

很明显，绝对值最小的规约数无法表达其和次小的规约数的差值，所以很容易导致有若干数字之间的差值下溢，可能会触发意料之外的后果。而如果采用非规约形式的浮点数，指数全0，偏移值比规约数偏移值大1（-126比-127大1），尾数小于1，那么非规约数能表达的最小值便是：

1
2
0.00..01 × 2^(-126) = 1 × 2^(-126-23)
                    = 2^(-149)

所以，非规约形式的浮点数解决了前述的突然式下溢出（abrupt underflow）而被标准采纳。

IEEE 754标准还规定了三个特殊值：

  1. 指数全0且尾数小数部分全 0，则这个数字为 ±0。（符号位决定正负）
  2. 指数为2e – 1且尾数的小数部分全 0，这个数字是 ±∞。（符号位决定正负）
  3. 指数为2e – 1且尾数的小数部分非 0，这个数字是 NaN。

结合前面的规约数，非规约数以及三个特殊值，可以得到如下总结：

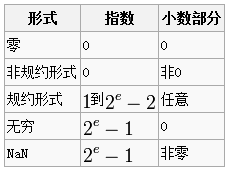
现在，让我们回忆一下，各种语言中普遍描述的双精度浮点数的范围：[-1.7 × 10-308, 1.7 × 10308]。打个岔，想象一个有 300 多位的十进制数字的适用情形，私以为远超过普通人想象力的边界。这个范围为什么是这个范围呢？我觉得，通过上面的讨论，大家应该能清晰，1.7 / 308 这些数字出现的必然原因。

首先，我们应该很容易根据偏移量得出双精度浮点数的计算公式：

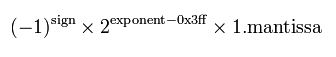
然后，以正数为例，按照上述 特殊值 中 ±∞ 和 NaN 的约定，指数的最大值应该满足指数取规约数的指数范围的最大值，然后小数部分取小数部分的最大值，可以得出这个二进制的数字应该是：

1
0 11111111110 11..11(52个)

转换为16进制表示：

1
0x7fef ffff ffff ffff

那么，根据前述规约数的原理，反编码便得到十进制的：1.7976931348623157 x 10^308。类似的道理，Sign位取反，便是范围的下限。

最后

为什么0.1 + 0.2 === 0.30000000000000004 ?

在浮点数运算中产生误差值的示例中，最出名应该是 0.1 + 0.2 === 0.30000000000000004 了，到底有多有名？看看这个网站就知道了http://0.30000000000000004.com/ 也就是说不仅是 JavaScript 会产生这种问题，只要是采用 IEEE 754 Floating-point 的浮点数编码方式来表示浮点数时，则会产生这类问题。下面我们来分析整个运算过程。

  1. 0.1 的二进制表示为 1.1001100110011001100110011001100110011001100110011001 1(0011)+ * 2^-4

  2. 当 64bit 的存储空间无法存储完整的无限循环小数，而 IEEE 754 Floating-point 采用 round to nearest, tie to even的舍入模式，因此 0.1 实际存储时的位模式是 0-01111111011-1001100110011001100110011001100110011001100110011010

  3. 0.2 的二进制表示为 1.1001100110011001100110011001100110011001100110011001 1(0011)+ * 2^-3

  4. 当 64bit 的存储空间无法存储完整的无限循环小数，而 IEEE 754 Floating-point 采用 round to nearest, tie to even的舍入模式，因此 0.2 实际存储时的位模式是 0-01111111100-1001100110011001100110011001100110011001100110011010

  5. 实际存储的位模式作为操作数进行浮点数加法，得到 0-01111111101-0011001100110011001100110011001100110011001100110100。转换为十进制即为 0.30000000000000004。